Tras la polémica decisión de la Comisión Europea el diario El Mundo tuvo a bien publicar una tribuna mía titulada La gestión de la estacionalidad. En ella describía aspectos sociales relacionados con el cambio de hora y concluía que difícilmente sin el cambio estacional la coordinación de la sociedad podía ser mayor de lo que es ahora. Creo que es conveniente que muestre en qué medida las sociedades gestionan de forma diferente el invierno y el verano.
Es, por supuesto, un (¡otro!) estudio basado las encuestas de empleo del tiempo y describe efectos a largo plazo del cambio. Es contrario a muchos otros estudios relacionados con el cambio estacional de hora, que se centran en sus dos molestas transiciones. Por ejemplo estudios sobre la influencia en el reloj biológico, en la toma de decisiones bursátiles, en accidentes o en aspectos relacionados con la salud como el infarto agudo de miocardio. Todos ellos aprovechan el «experimento natural» que muchos gobiernos ponen a su disposición cuando se altera la hora oficial. Estos efectos a corto plazo suscitan preocupación hoy en día y retroalimentan las molestias que todos percibimos en las transiciones.
Cinco de las ocho encuestas de empleo del tiempo que analicé proporcionan datos que permiten estudiar la estacionalidad de la sociedad. Son las relativas a países importantes: Estados Unidos, España, Italia, Francia y Reino Unido, listados en orden creciente de latitud. En este estudio no he incluido encuestados de Canarias, los departamentos franceses de ultramar y las partes no contiguas de Estados Unidos.
He divido la encuesta en dos semestres: abril-septiembre y octubre-marzo. Identificaré al primero como «verano» y al segundo «invierno». Ambos semestres coinciden prácticamente con los periodos de aplicación de la hora de verano y de invierno. He descartado cambiar el mes de octubre del segundo grupo al primero, siguiendo la regulación horaria, porque produce una división no equitativa de la muestra… y porque no podía hacerlo en España e Italia.
En esta entrada analizaré la actividad laboral. En la siguiente entrada haré lo mismo para el ciclo de sueño/vigilia. Como anteriormente hice he usado las mismas cinco estadísticas relacionadas con la actividad laboral. Dos usan el tiempo relativo a una referencia, dependen de la hora legal, se expresan en hora local y se pueden relacionar con el amanecer y el anochecer:
- Entrada al trabajo.
- Salida del trabajo.
Las otras tres son intervalos de tiempo y no están (deben estar) relacionadas con la hora legal o con el cambio estacional:
- La amplitud laboral: el tiempo que pasa entre la entrada y la salida.
- La duración de la jornada laboral: cuánto tiempo diario se emplea en trabajar.
- Las pausas, definidas como la diferencia entre amplitud y duración.
A diferencia del análisis anterior en este no he incluido a los encuestados que están trabajando a las 4am ya que causan pequeños problemas a la hora de definir estas estadísticas, excepción hecha de la duración del trabajo. Esta exclusión reduce ligeramente el tamaño de las muestras.
Antes de describir los resultados haré una descripción técnica del análisis. Quien no esté interesado en el howto puede saltárselo e ir directamente a los resultados.
Técnica matemática: análisis PP y análisis QQ
Las encuestas de empleo del tiempo dividen un día (1440 minutos) en 144 momentos de 10 minutos de duración. Las estadísticas resultantes tienen por tanto ese nivel de discretización.
El tamaño de la muestra N es del orden miles de encuestas y podemos asimilarlo a haber lanzado un dado, o mejor dicho un sólido regular de 144 caras, si tal cosa existiese, miles de veces. Hay diferencias evidentes. El lanzamiento del «dado» produciría, aproximadamente, el mismo número de casos para todos los resultados. Pero no nos comportamos así, elegimos ciertas horas para entrar a trabajar y ciertas para salir. Desdeñamos otras. Así en las encuestas de empleo del tiempo hay muchos casos en unos determinados momentos y pocos en otros.
Del lanzamiento múltiple de ese «dado» se pueden extraer propiedades descriptivas como el número de ocurrencias de cada resultado, el valor medio de los resultados, la desviación mediana o los cuartiles. También con las encuestas de empleo del tiempo, para cada una de las cinco estadísticas. Es lo que he venido analizando desde hace unos años. Por ejemplo esto tan reciente.
También se puede obtener lo que llamamos probabilidad acumulada empírica que sería el número de resultados menores o iguales que uno dado. Cuántas veces la tirada del dado ha resultado en 42 o menor. En las encuestas de empleo del tiempo esta probabilidad acumulada es preguntarse cuántos trabajadores ya han entrado a las 08:10 o cuántos tiene una jornada laboral de 07h40m o menor. Aquí hay un ejemplo en la figura de la derecha.
Con N tiradas de ese dado de 144 caras puedo plantar el siguiente problema: hacer dos extracciones, una de tamaño N1 y otra de tamaño N2, de forma que N=N1+N2. Calculamos las propiedades descriptivas de esas extracciones (media, cuartiles, desviación típica, probabilidad acumulada…). Es un hecho pertinaz estas propiedades presentarán valores diferentes para las dos extracciones.
Si el dado fuera perfecto, la muestra fuera muy grande y las extracciones también las diferencias llegarían a ser muy pequeñas: en el caso de muestras infinitas, nulas. Alternativamente el análisis de esas diferencias permite discernir si el dado es ideal o tiene algún tipo de sesgo. Este discernimiento no viene determinado por cómo de grande son las diferencias sino por cómo de grande lo son en relación con el tamaño de la muestra.
No voy a hacer un extracción aleatoria en las encuestas. Todo lo contrario. Haré una extracción sesgada: de una parte analizaré a quienes responden en invierno, de otra parte a quienes responden en verano. La amplitud de las desviaciones en relación con el tamaño de la muestra permitirá discernir si son pequeñas o grandes. Si son pequeñas concluiremos que se trata de ruido aleatorio o que el comportamiento en verano es igual que en invierno. Si son grandes detectaremos sesgos.
El análisis de la diferencia de valores medios no planeta muchos problemas: es solo restar dos resultados y contextualizarlos con el tamaño de cada muestra y la desviación típica de cada muestra. Se pasan los datos por la prueba t de Welch y se obtiene un resultado que ayuda a discernir si hay sesgo.
La diferencia o desviaciones en la probabilidad empírica acumulada es algo más rica. La siguiente figura muestra a la izquierda dos probabilidades empíricas representadas frente al tiempo. Está discretizadas a 144 valores por día o un valor cada diez minutos.
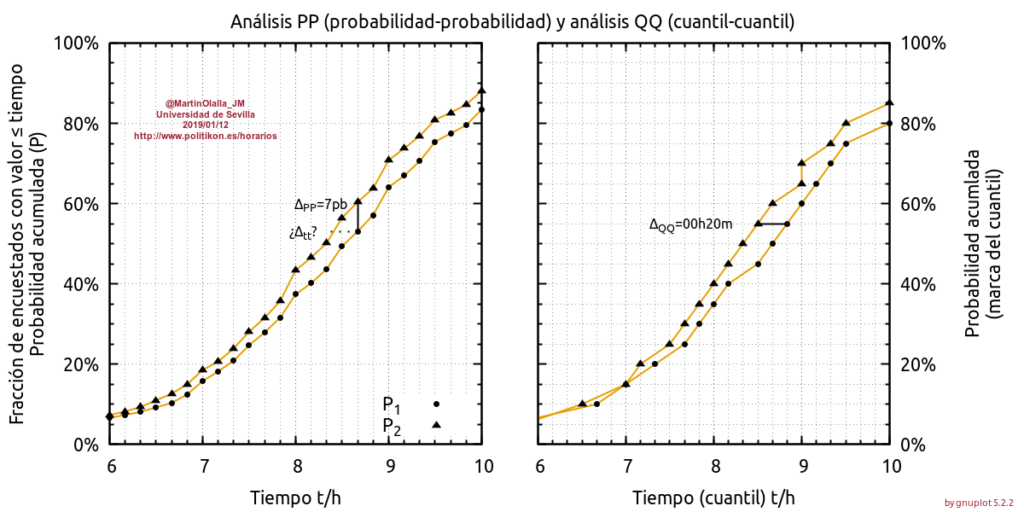
Figura 1. A la izquierda dos distribuciones empíricas a modo de ejemplo. El análisis PP (izquierda) reporta la diferencia vertical entre ellas. En esta gráfica los puntos (discretos) se sitúan sobre la malla vertical y no casan horizontalmente. A la derecha la gráfica de cuantiles y el análisis QQ. Los puntos se disponen de forma de que coincidan con la malla horizontal (un punto por cuantil) y permite reportar diferencias temporales entre cuantiles. En el caso de una distribuciones discretas, como la mostrada en la figura, los puntos también pueden coincidir con la malla vertical. Los cuantiles mostrados se corresponden con los vigentiles.
La desviación ΔPP=P2-P1 es la distancia vertical entre dos puntos situados en el mismo tiempo. Si P se mide en porcentaje, como en la figura, la diferencia se expresa en puntos básicos.
Las probabilidades acumuladas son monótonas crecientes (es decir, siempre crecen). Por eso el signo de la desviación determina si una distribución se adelanta o retrasa sobre la otra. En el caso representado Δ es positivo lo que implica que P2 se adelanta, como se observa en la figura. Una ventaja de computar estas desviaciones ΔPP (análisis PP) es que podemos hacer este análisis a lo largo del día: ver cuándo se adelanta y cuándo se atrasan las distribuciones.
Estrictamente para ver si una probabilidad se adelanta sobre la otra hay que computar la distancia horizontal, Δtt. No puede hacerse directamente porque los puntos solo casan verticalmente, no lo hacen horizontalmente. Hay que calcular la distribución de cuantiles y, a partir de ella, determinar la distancia horizontal (diferencia de cuantiles) entre las dos distribuciones (figura de la derecha). Es el análisis QQ. Es un método indirecto que exige una construcción previa pero es más fácil expresar y entender cosas como «el percentil 60 se adelanta 20min», en vez de «la probabilidad acumulada crece 7pb para t=08h40m».
El tamaño de la muestra entra en el análisis PP definiendo la cantidad K=ΔPP×√N, donde N es el el promedio armónico del tamaño de las dos muestras. Si K es suficientemente grande las desviaciones son suficientemente grandes como para podamos hablar de sesgo sistemático. Si K es suficientemente pequeño lo más probable es que las desviaciones no sean más que ruido aleatorio: el tipo de desviaciones que obtendríamos comparando dos extracciones de un conjunto de tiradas de un dado perfecto.
Esta es la idea de la estadística de Kolmogorov-Smirnov (KS) . Habitualmente K se expresa en forma de número probabilístico p=exp(-K2) pero esto solo tiene un sentido preciso si las distribuciones fueran continuas y no es nuestro caso. Aún así voy a definir el umbral arbitrario u=√(-log(0.05))≈1.731 para discriminar desviaciones grandes (K>u) de desviaciones pequeñas (K<u). El umbral simula el nivel p=0.05 habitual en este tipo de análisis pero debido a la discretización no tiene el significado habitual. En los casos continuos el nivel p=0.05 indica que solo un 5% de las extracciones aleatorias producirían desviaciones tan grandes como el K observado, lo que se suele admitir como presencia de sesgo (a nivel p=0.05).
Desviaciones en los valores medios
En este enlace pueden ver las desviaciones de los valores medios en las 25 estadísticas analizadas. La desviación está calculada como valor medio estival menos valor medio invernal. Desviaciones positivas de la entrada/salida indican que se adelanta en verano; desviaciones negativas que se atrasa. Para las amplitudes/pausa/duración desviaciones positivas significa cantidades mayores en verano; desviaciones negativas, lo contrario. Entre paréntesis aparece el error estadístico muestral de la desviación del valor medio.
En color negro aparecen las desviaciones que sobrepasan el nivel p=0.05 en la prueba t de Welch, una versión de la prueba t de Student para muestras con tamaño y desviación típica diferentes. Solo 2 de 25 análisis sobrepasan el umbral y aparecen en negro en el cuadro. Esto quiere decir que solo en dos casos podemos estar razonablemente seguros de que el invierno es diferente del verano. El problema es que esta tasa (8%) es solo muy ligeramente superior a lo que cabría esperar para extracciones aleatorias de cada encuesta al nivel p=0.05, es decir 5%.
Los valores del cuadro están expresados en minutos. Las desviaciones alcanzan, como máximo, 7 minutos. Por ejemplo, la entrada al trabajo en España se adelanta de media esa cantidad.
Solo son posibles dos conclusiones: o bien los valores medios de los parámetros de la actividad laboral son estables estacionalmente, o bien las muestras analizadas no se corresponden a invierno/verano sino que son dos extracciones aleatorias.
Desviaciones en la probabilidad acumulada
El resultado anterior es ciego: no permite saber cómo evolucionan las diferencias en el intradía. El análisis PP permite mostrar estas evoluciones. La siguiente figura muestra las desviaciones P(verano)-P(invierno) para las estadísticas relacionadas con la jornada laboral en España.
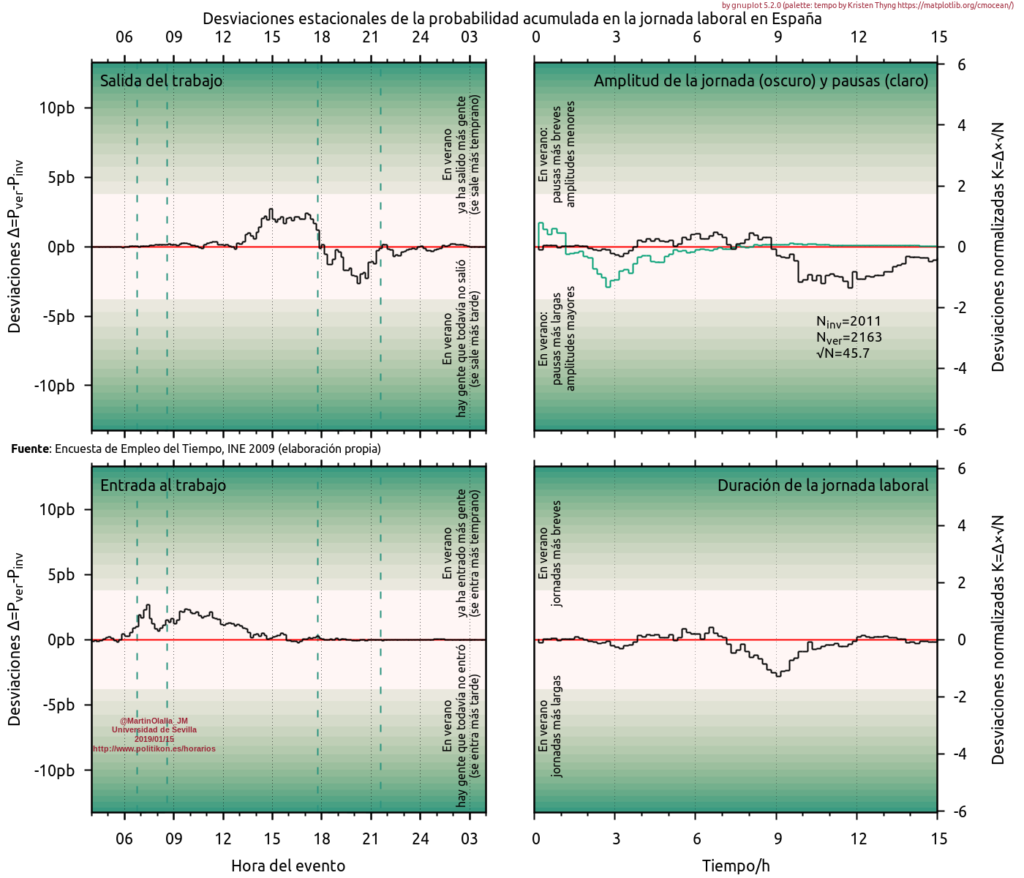
Figura 2. Desviaciones verano-invierno en la jornada laboral española. La banda de color más claro representa el umbral u=√(-log(0.05))≈1.731 e indica el rango en el que las desviaciones probablemente no son estadísticamente significativas. A la izquierda la entrada (abajo) y salida (arriba) del trabajo contextualizadas con el amanecer y anochece estival e invernal (líneas verticales quebradas). A la derecha la duración de la jornada laboral (abajo) y la amplitud y duración de las pausas (arriba). La entrada al trabajo se adelanta particularmente en la parte del día en la que hay luz en verano pero oscuridad en invierno. La salida del trabajo se adelanta en verano antes de las 18 (hora del anochecer invernal). A de esa hora se retrasa hasta que a la hora del anochecer estival se equilibran. Las pausas cortas (menores de una hora) y las jornadas no muy amplias (menores de nueve horas) tienden a acortarse en verano mientras que las pausas largas (mayores de dos horas) y amplitudes grandes (mayores de nueve horas) tienden a alargarse.
No son gráficos fáciles de interpretar. El eje X es un día (un ciclo). A la izquierda en forma de hora local de 4am a las siguientes 4am. A la derecha intervalos de tiempo desde 0 a 15h. En el eje vertical la diferencia entre las probabilidades acumladas en verano e invierno. El eje vertical se dispone de forma simétrica alrededor de 0 que es el punto de equilibrio. Las curvas empiezan siempre en el valor 0 y terminan en el valor 0. A lo largo del día hay excursiones positivas o negativas. Cada gráfica tiene una pequeña leyenda explicando el significado de cada excursión. El eje vertical aparece expresado en puntos básicos a la izquierda mientras que a la derecha se expresa en forma de distancia normalizada. Cualesquiera de los dos vale para cualesquiera de las gráficas.
Las dos gráficas de la izquierda pueden contextualizarse con la actividad solar. Las líneas verticales discontinuas muestra los amaneceres y anocheceres extremos: verano e invierno.
El fondo de color muestra diferentes valores de K. El fondo más claro y más pequeño representa el umbral u=1.731 explicado antes. En ningún caso las desviaciones españolas lo sobrepasan. Probablemente todas las desviaciones son poco relevantes desde un punto de vista estadístico y entra dentro de lo posible que haya confundido las submuestras y en vez de comparar invierno con verano esté comparando dos extracciones aleatorias de trabajadores encuestados.
Sin embargo, para ser una extracción aleatoria se comporta de forma muy sistemática. La entrada al trabajo se adelanta en verano cerca del amanecer estival. Cuando hay luz en verano pero no en invierno. Este adelanto se superpone constructivamente al adelanto previo de la hora oficial y muestra que, a pesar de este, hay gente que quiere o que necesita adelantar más el inicio de la jornada laboral.
La salida del trabajo se adelanta a las 3pm (antes no sale casi nadie, ni en verano ni en invierno). Quizá muestre jornadas que en invierno son partidas y en verano son de tipo continuo, adelantando la entrada y salida del trabajo.
Este adelanto se mantiene hasta las 5pm cuando la desviación disminuye porque hay más gente en invierno que sale a esa hora que en verano. Normal, algunos de los que salen a las 5pm en invierno ya han salido a las 3pm en verano. A las 6pm (hora del anochecer invernal) la situación ha vuelto al equilibrio. A las 7pm, también.
A partir de entonces el verano se retrasa respecto del invierno. La gente tarda más en salir. En este momento es de noche solo en invierno. Todo muy lógico. A las 20:20 se alcanza la desviación máxima en ese sentido (Δ=-2.6pb). A partir de ahí se retorna al punto de equilibrio: sale más gente en verano que en invierno, porque queda más gente trabajando. El equilibrio se alcanza a la hora del anochecer estival: el inicio de la noche perpetua.
En la estadística de pausas se observar que hay más encuestados con pausas menores de una hora en verano, probablemente a causa del proceso explicado anteriormente. Quienes tienen pausas superiores a dos horas suelen aumentar la pausa. Es decir el fin de jornada se retrasa a costa de ampliar las pausas y no tanto de ampliar la duración de la jornada laboral, que por otra parte se amplía en cierta medida.
Todas las desviaciones que he ido glosando son mínimas desde cualquier punto de vista, como las desviaciones de los valores medios. Por eso la figura 2 muestra una escala vertical tan generosamente amplia.
Sin embargo, y con mucha cautela, no dejo de asombrarme de estos resultados: la evolución intradía de las desviaciones estacionales reproduce casi al momento cómo una parte pequeña de la actividad laboral se ajusta estacionalmente evitando la insolación del mediodía estival o favoreciendo jornadas continuas. Es un patrón de comportamiento perfectamente razonable dadas las condiciones geográficas del país y que no se observa en otros lugares. Entiendo que esto puede ser una casualidad (una extracción aleatoria de la encuesta produce esta figura y otras muchas, hay del orden de 10103 extracciones posibles), pero podría ser también que la encuesta de empleo del tiempo esté realmente bien hecha y que tengamos esos hábitos estacionales.
Este patrón lo esbocé en esta tribuna en el diario El País. Entonces lo hice recordando dos observaciones cotidianas locales: (1) el hecho de que el sector de la construcción tiene que adelantar la entrada al trabajo en verano para lo cual se firman convenios fomentados por las autoridades competentes, (2) el hecho de que el comercio local en Sevilla retrasa generalmente la apertura en las tardes estivales, compensando el adelanto de hora estacional.
He realizado las gráficas correspondientes al resto de países analizados: Italia, Francia, Reino Unido, y Estados Unidos. Cada una cuenta su historia, distinta de la española.
Aquí se muestran las distribuciones de entrada y salida del trabajo de los cinco países en forma de 2 filas por 5 columnas. La ordenación de los países por latitud permite esbozar tendencias muy indiciarias con desviaciones disminuyendo conforme se aumenta la latitud (movimiento hacia la derecha en la figura).
Desviaciones máximas PP y QQ
La evolución intradía es interesante desde un punto de vista social pero como he ido indicando puede estar sujeta a variaciones. Desde un punto de vista matemático lo relevante son los valores máximos (diarios) de esas desviaciones. Los he tabulado de forma análoga a las desviaciones de los valores medios y puede acceder a ellos en este enlace.
Todas las distribuciones analizadas, excepto una, producen desviaciones menores que el umbral. La estadística díscola (entrada al trabajo en Italia) tiene un K=1.9 muy próximo al umbral fijado. Su pval equivalente es 0.027. También produce una de las dos desviaciones significativas del valor medio.
Estas desviaciones máximas tan pequeñas siguen siendo una muestra del grado de coordinación social entre invierno y verano, es decir de nuestra apetencia por horarios estables anualmente. Alternativamente podría ser que estuviera analizando extracciones aleatorias.
El signo de las desviaciones máximas de la entrada al trabajo es positivo: ocurren en el sentido de adelantar la entrada al trabajo en verano. La hora a la que ocurren estas desviaciones máximas y el valor de P lo circunscriben a la primera mitad de trabajadores que entra más temprano. En España a las 07:30 ha entrado el 20% de encuestados estivales frente a el 17% de encuestados hiemales. A esa hora es de día en verano y de noche en invierno. La desviación máxima entre cuantiles en España es de 20min pero ocurre en el otro extremo de la entrada al trabajo: las 09:50 para el percentil 80. Estos adelantos se superponen constructivamente al adelanto de la hora oficial y expresa la actividad laboral que no puede permitirse el lujo de empezar a trabajar muy lejos del amanecer.
En Francia la desviación máxima PP es negativa (retraso estival) pero es contemporánea con un adelanto anterior, que se puede observar en el percentil 24, adelantado diez minutos en verano: 07:40 frente a 07:50.
En Reino Unido la desviación es claramente menor (K=0.7) lo que puede indicar que sea menos sensible al amanecer. Una hipótesis es que el amanecer se expande durante un rango de cinco horas y la actividad humana no puede seguirlo de forma tan eficaz como a la latitud de la península ibérica. O que no hay necesidad de ello. Es decir, se pueden permitir el lujo de empezar después del amanecer estival porque este ocurre muy temprano y luego no hay una insolación tan importante a mediodía.
En la salida al trabajo la desviación máxima también es positiva, salvo en Estados Unidos pero, en este caso, ocurre en la cola de la distribución. En España e Italia ocurre sobre el primer tercio/quinto de trabajadores. En España un 31% de trabajadores ha salido a las 15:00 en verano frente a un 28% en invierno. Una desviación máxima de 3pb. En cuantiles la desviación máxima es de 40 minutos. El percentil 40 se sitúa a las 17:00 en invierno y solo a las 16:20 en verano.
En Reino Unido y Francia la desviación máxima es un efecto casi de cola (P=80% y P=7%), lo que indica que la salida del trabajo es más estable para la mayoría de casos.
El resto de estadísticas se refieren a intervalos de tiempo y no dependen de la hora oficial. En España las tres desviaciones máximas ocurren en la cola final para P>80% y valores altos de las magnitudes, siempre en el sentido de amplitudes, jornadas y pausas más largas en verano. La desviación máxima entre cuantiles de la pausa ocurre para el percentil 44: el 44% de encuestados tiene 20min de pausa en invierno frente a 0 en verano. Es reflejo de la desviación positiva de las pausas en el tramo de pausas menores de una hora.
Finalmente la desviación estacional de los cuartiles (percentil 25, 50, y 75) puede verse en este enlace.
Conclusión
El ciclo de trabajo está prácticamente sostenido por el reloj local mostrando desviaciones mínimas de invierno a verano a pesar del cambio de hora estacional. O bien tenemos unas anteojeras anchas y toleramos dócilmente los cambios estacionales de la hora, como robots siguiendo locamente a un metrónomo loco… o bien… todo lo contrario: la cambio de hora ayuda a genera esa estabilidad, al menos a nuestras latitudes. Esta sería una de las utilidades de esta práctica moderna. Detecten la ironía en la idea inicial: realmente las sociedades no toleran cambios arbitrarios en la regulación de la hora legal. La historia da pruebas de ello.
Los resultados indicarían que el cambio de hora gestiona la estacionalidad de las sociedades modernas que así funcionan con horarios estables anualmente (medidos en hora local), a la vez que variables estacionalmente (medido en hora universal). La ausencia de desviaciones significativas hace que la actividad laboral se adelante una hora en verano (medido con un reloj atómico), aprovechando el adelanto del amanecer.
La alternativa a este esquema es que los horarios varíen estacionalmente. No se puede predecir en qué medida lo harían si la práctica del cambio de hora se elimina, sí que las desviaciones estacionales que inducirían serían mayores que las que se miden actualmente con el reloj local. Esto debe producir problemas de descoordinación entre diferentes capas de la sociedad, incluido a nivel familiar.
En la próxima entrada (que será próxima) reproduciré este análisis para el ciclo de sueño/vigilia. Es un análisis aún más interesante porque este ciclo sí produce variaciones estacionalmente significativas.
Feliz y próspero año 2019 a todos
