En las últimas semanas han aparecido en la prensa noticias alarmantes sobre el aumento del alcance de los misiles norcoreanos, junto con la posibilidad de que puedan transportar armas nucleares y que estas lleguen a la costa oriental americana o a la península ibérica. El asunto ha sido objeto de memes en las redes sociales.
Las grandes posibilidades gráficas modernas permiten hacer un gráfico que explica fácilmente la situación. Por ejemplo este, tomado de la wikimedia:
Proyección acimutal equidistante centrada en Corea del Norte y mostrando el alcance de diferentes misiles. Autor TUBS.
Lo que ven en la figura es una proyección acimutal centrada en Corea del Norte y círculos concéntricos alrededor de ella que representan puntos equidistantes al país asiático. Mi propósito en esta entrada es explicarles cómo hacer estos círculos y en qué medida está relacionado con el amanecer y el anochecer.
La proyección acimutal es como ver a la Tierra desde arriba. No estamos acostumbrados a ver proyecciones acimutales centradas en un punto cualquiera pero tal vez no resulte muy extraña una proyección acimutal polar. Es lo que aparece en la bandera de Naciones Unidas.
En este tipo de proyecciones un punto y su antípoda hacen de «polos» de la Tierra. Una propiedad peculiar de la esfera es que podemos unir dos puntos antipodales por una infinidad de arcos de circunferencias diferentes. Es algo extraño porque estamos habituados a las propiedades del plano donde dos puntos solo pueden unirse por un único segmento recto. Esa pluralidad de arcos de circunferencias que unen dos puntos antipodales reciben el nombre de círculos máximos, geodésicas o podemos identificarlos aquí como meridianos. En la proyección acimutal los meridianso aparecen como un haz de rectas que pasan por el centro de la proyeccion, como se ve en la bandera de Naciones Unidas. Los meridianos indican siempre la dirección o rumbo y es una convención muy útil que los que estamos habituados a manejar se hayan definido a partir de los puntos antipodales que pasan por el eje de rotación del Tierra: son los dos únicos puntos de la Tierra que no rotan y permiten orientarnos de forma eficiente.
El círculos concéntricos que aparecen en la proyección acimutal señalan distancias lineales o angulares al centro de la proyección. En el mapa de Naciones Unidas los reconocemos como paralelos y señalan la latitud ϕ o la colatitud (90°-ϕ), que es la distancia angular al Polo Ártico. En el mapa centrado en Corea del Norte aparecen distancias. La relación entre ambas puede obtenerse con este sencillo argumento: un arco de 10° de una circunferencia de R=6371km (el radio de la Tierra) tiene una longitud lineal de 10°πR/180°=1111km. El paralelo 80° está situado, por tanto, a 1111km del Polo Ártico y un misil que recorra 1111km a lo largo de un meridiano abarcará 10°.
En la proyección norcoreana de la wikimedia se pueden ver, con una tinta muy clara, como son los paralelos y meridianos estándares vistos desde Corea del Norte. Es decir cómo se deforman los meridianos y paralelos con los que hemos cuadriculado la Tierra y que están centrados en los polos que pasan por el eje de rotación de la Tierra.
Y la cuestión es precisamente cómo saber la distancia y rumbos entre dos puntos de la Tierra sabiendo sus respectivas latitudes y longitudes convencionales. Solo respondiendo a esta pregunta podemos trazar una circunferencia que dista 4000km de silo de misiles norcoreano.
Una forma de obtener la respuesta es construir un triángulo (esférico) constituido por dos puntos de la Tierra cualesquiera (escojamos al azar Teherán y Pyongyang) y uno de los polos, por ejemplo el polo Ártico. Los dos lados del triángulo que pasan por el polo Ártico son simplmente el arco de meridiano que lo une con las ciudades elegidas y su amplitud es la colatitud de las ciudades. El tercer arco une ambas ciudades y queremos saber su amplitud.
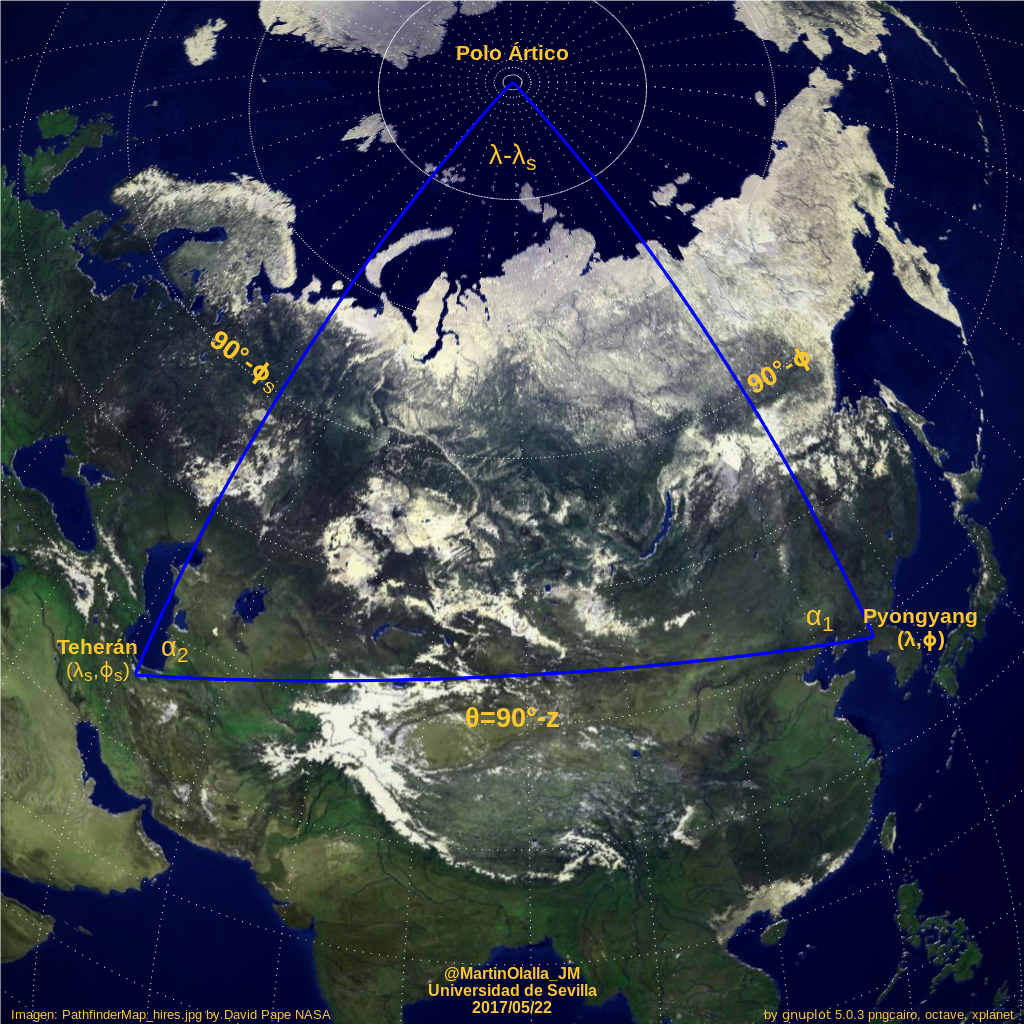 Proyección ortográfica que muestra el triángulo esférico formado por el polo Ártico y las ciudades de Pyongyang y Teherán. Los lados del triángulo son arcos de círculos máximos (meridianos; centrados en el centro de la Tierra). La amplitud de los arcos que pasan por el polo está relacionada con la latitud de las ciudades. La amplitud del tercer arco está relacionada con la distancia entre ambas ciudades. El ángulo cuyo vértice es el polo Ártico es la diferencia de longitud geográfica entre las ciudades y los otros dos ángulos interiores indican el rumbo para ir de una ciudad a la otra. Al salir de Pyongyang hacia Teherán se toma un rumbo WNW. Al salir de Teherán hacia Pyongyang se toma rumbo ENE; obsérvese que no son rumbos contrarios.
Proyección ortográfica que muestra el triángulo esférico formado por el polo Ártico y las ciudades de Pyongyang y Teherán. Los lados del triángulo son arcos de círculos máximos (meridianos; centrados en el centro de la Tierra). La amplitud de los arcos que pasan por el polo está relacionada con la latitud de las ciudades. La amplitud del tercer arco está relacionada con la distancia entre ambas ciudades. El ángulo cuyo vértice es el polo Ártico es la diferencia de longitud geográfica entre las ciudades y los otros dos ángulos interiores indican el rumbo para ir de una ciudad a la otra. Al salir de Pyongyang hacia Teherán se toma un rumbo WNW. Al salir de Teherán hacia Pyongyang se toma rumbo ENE; obsérvese que no son rumbos contrarios.
Ese tercer arco es también un meridiano, aunque no pase ni por el polo Ártico ni por el Antártico. Es uno de los meridianos que unen Teherán con su punto antipodal y, también es uno de los meridianos que unen Pyongyang y su punto antipodal. Mejor dicho: es el único meridiano que une Teherán, Pyongyang y sus respectivos puntos antipodales. Su amplitud viene determinada por una fórmula larga llamada ley de los cosenos de la trigonometría esférica:
cosθ=sinϕsinϕs+
Esta fórmula vale para cualesquiera dos puntos de la Tierra y da la distancia angular entre ellos. Se puede convertir en distancia lineal con el cálculo D=πRθ/180°. En esta página pueden poner sus dos puntos preferidos y ver esas distancias. Para Pyongyang y Teherán salen 6386km que corresponden a un ángulo de unos 57°. El rumbo de salida de Pyongyang es 292° (α1=68°) y el de salida de Teherán 62° (α2=62°). En la página usan la fórmula de los semiversenos y es que llega un momento en la vida cuando uno se entera de que existen cosas llamadas verseno y semiverseno, coverseno y semicoverseno.
Si fijamos uno de los puntos, por ejemplo ponemos λ y ϕ con los valores correspondientes a un silo de misiles y ponemos una amplitud determinada, por ejemplo θ=10° la ecuación anterior es el compás que nos dibuja la circunferencia situada a 10° (1111km) del silo.
La circunferencia situada a 10000km está a 90° de distancia angular; los más viejos recordarán que el metro se definió como la diezmillonésima parte del cuadrante de un meridiano terreste. Pues un cuadrante es la cuarta parte de una circunfencia, es decir un arco de 90°, y 10000km son exactamente diez millones de metros.
Ahora voy a olvidarme de los misiles norcoreanos y voy a jugar a proyectar el cielo sobre la Tierra y la Tierra sobre el cielo. Voy a recordar que en todo instante hay un punto de la Tierra, lo llamamos punto subsolar, en el que los rayos solares inciden verticalmente y no producen sombra. El Sol ocupa en el cénit celeste en el punto subsolar. Este punto varía constantemente: la variación de su longitud geográfica es lo que permite definir el Tiempo Universal Coordinado, es decir, la hora del día. La variación de la latitud del punto subsolar a lo largo del año determina la estación del año. También hay en cada instante un punto sublunar, un punto submarciano, subvenéreo, subjoviano, etcétera, que son menos importantes que el subsolar… excepto el punto subestrellapolar que actualmente cae sobre el polo Ártico. Por eso observamos a la Estrella Polar quieta en el cielo y sirve para marcar una dirección y orientárnos. Ver la Estrella Polar en el cielo es una forma de ver dónde está el Polo Ártico (siempre está en el mismo sitio) y ver el Sol en el cielo es una forma de ver dónde está el punto subsolar (éste sí va cambiando a lo largo del tiempo).
Si hacemos una proyección acimutal centrada en el punto subsolar los círculos concéntricos nos servirían para marcar distancias lineales al centro. Sin embargo ahora es más interesante verlo angularmente: si en el centro de la proyección el Sol ocupa el cénit entonces conforme nos alejamos de ese centro el Sol va disminuyendo progresivamente su altitud en el cielo, lo que podemos medir con un cuadrante y expresarlo angularmente.
Así los círculos concéntricos indicarán la distancia angular entre el Sol y el cénit. Esto permite conocer la amplitud de las sombras y, en general, la insolación. Como apunte histórico puedo añadir que Eratóstenes midió la Tierra siguiendo estas ideas. De una parte midió la distancia entre Alejandría y Siena, digamos que caminando. De otra parte sabía que en instante del año Siena es el punto subsolar y, en ese momento, midió la posición angular del Sol en el cielo de Alejandría con ayuda de las sombras que proyectaba. A partir de ahí pudo determinar el radio de la Tierra y lo hizo muy bien.
Tanto si queremos medir sombras como si queremos medir insolación lo importante es el valor del coseno del ángulo que forma el Sol con el cénit θ. El coseno de ese ángulo (cosθ) viene dado también por la ley de cosenos esférica en la que uno de los puntos es el punto subsolar. Con ella se puede determinar la hora del amanecer, anochecer, crespúsculos y, en general, posicionar al Sol en el cielo cualquier día del año, a cualquier hora del año en cualquier lugar de la Tierra. Conocer la evolución del factor coseno y su dependencia de parámetros orbitales es importante para entender el comportamiento climático de la Tierra o, a escala menor, para diseñar y colocar captadores de energía solar.
Voy a describir lo relativo a los amanecer y anocheceres que ocurren cuando nos alejamos lo suficiente del punto subsolar como para que el Sol alcance el horizonte y se sitúe a θ=90° del cénit. En distancia lienal eso sigue correspondiendo a 10000km: el punto subsolar se encuentra siempre a 10000km de distancia de un observador sobre el que amanezca o anochezca. A menos distancia es de día, a más distancia es de noche.
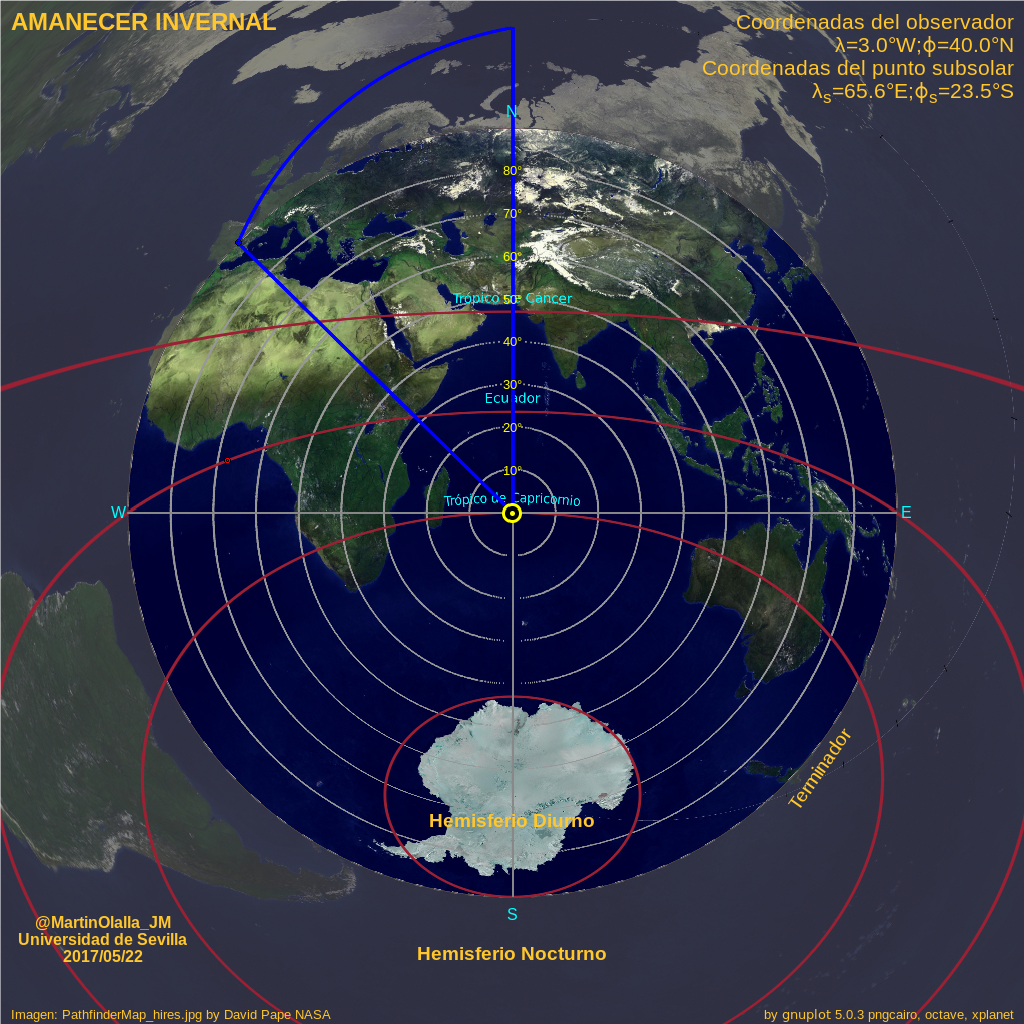 Proyección acimutal centrada en el punto subsolar cuando sus coordenadas son ϕs=23.5°S (solsticio de invierno) y λs=65.5°E (UTC=12h-65.6h/15=7.6h=07:37). La imagen muestra el hemisferio iluminado de la Tierra y a 90° (10000km) del punto subsolar el terminador que separa la noche del día. Sobre el terminador está amaneciendo o anocheciendo. El triángulo en azul lo forman el polo Ártico, el punto subsolar y la ciudad conquense de Tarancón, donde está amaneciendo. Sobre su antípoda, en Nueva Zelanda, está anocheciendo y es verano.
Proyección acimutal centrada en el punto subsolar cuando sus coordenadas son ϕs=23.5°S (solsticio de invierno) y λs=65.5°E (UTC=12h-65.6h/15=7.6h=07:37). La imagen muestra el hemisferio iluminado de la Tierra y a 90° (10000km) del punto subsolar el terminador que separa la noche del día. Sobre el terminador está amaneciendo o anocheciendo. El triángulo en azul lo forman el polo Ártico, el punto subsolar y la ciudad conquense de Tarancón, donde está amaneciendo. Sobre su antípoda, en Nueva Zelanda, está anocheciendo y es verano.
La figura anterior está realizada para el momento en que amanece en invierno sobre Tarancón, una ciudad situada en el centro geográfico de la península Ibérica. El triángulo en azul señala el triángulo esférico formado por el polo Ártico, el punto subsolar y la ciudad conquense (similar al triángulo esférico formado por Pyongyang, Teherán y el polo Ártico). El lado que une el punto subsolar y la ciudad indica qué rumbo tenemos que tomar desde el punto subsolar para ir a dicha ciudad: que sea recto indica que es un arco de meridiano que une el punto subsolar y la ciudad como señalaba al explicar el triángulo formado por Pyongyang, Teherán y el polo Ártico.
Merece la pena ver la proyección acimutal centrada en la ciudad para ver por dónde parece el Sol cuando amanece sobre la ciudad. En este caso con rumbo SE:
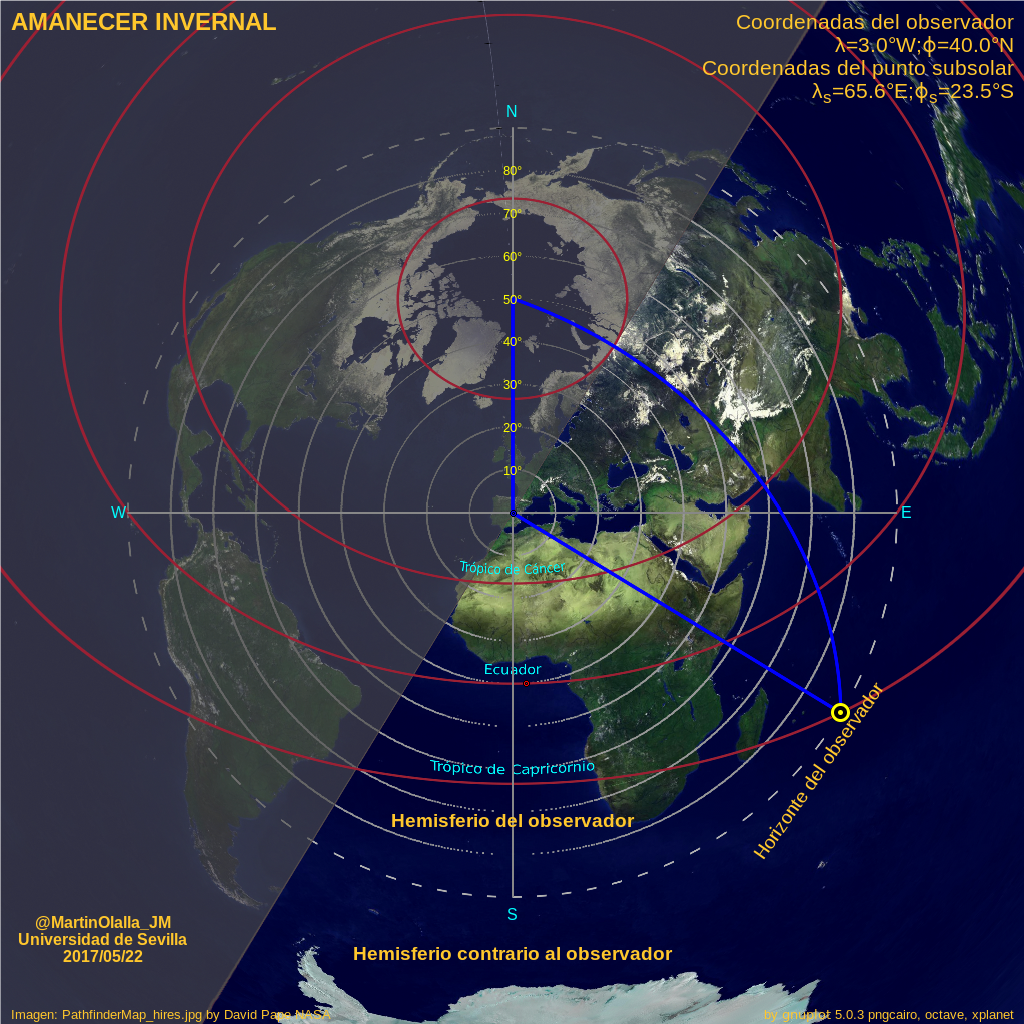 Proyección acimutal centrada en Tarancón cuando amanece en verano estando el punto subsolar en ϕs=23.5°S (solsticio de invierno) y λs=65.6°E. El punto subsolar al amanecer se encuentra a 90° (10000km) del centro de la proyección. El rumbo de salida del Sol es SE.
Proyección acimutal centrada en Tarancón cuando amanece en verano estando el punto subsolar en ϕs=23.5°S (solsticio de invierno) y λs=65.6°E. El punto subsolar al amanecer se encuentra a 90° (10000km) del centro de la proyección. El rumbo de salida del Sol es SE.
Pero también podemos describir sobre esta figura el recorrido del punto subsolar durante el día de invierno. Amanece cuando el punto subsolar en medio del océano Índico a 10000km de Tarancón y conforme la Tierra rota el punto subsolar se acerca a Tarancón a lo largo del trópico de Capricornio y el Sol se eleva en el cielo. A mediodía alcanza su distancia mínima y altura máxima. Observe que en ese momento el Sol está quieto en el cielo porque su distancia al cenit cambia más lentamente. El Sol está virando y pasa de ir creciendo a ir decreciendo conforme el punto subsolar se aleja de Tarancón. Finalmente el Sol se pone cuando el punto subsolar está cerca Antofagasta con λs=71.6°W (UTC=12h+71.6h/15=16.7=16:46) de nuevo a 10000km de distancia.
Finalmente podemos describir con esta imagen cómo cambia el amanecer y el anochecer al avanzar el año y crecer la latitud del punto subsolar. Al crecer la latitud del punto subsolar se acerca a la latitud de Tarancón y para mantener los 10000km de distancia al amanecer es necesario que la longitud del punto subsolar se aleje de Tarancón en el instante del amanecer. Y como longitud geográfica es tiempo, la hora del amanecer se va adelantando progresivamente. En verano llega a amanecer cuando λs=108.4°E (04:46UTC) cerca de Hong Kong y el rumbo de salida del Sol es ya NE. Correspondientemente la longitud del punto subsolar al anochecer se aleja progresivamente y la hora del anochecer se retrasa hasta que, en verano, ocurre cuando λs=114.4°W (19:37UTC), con rumbo NW, cerca de la punta de Baja California.
La región de los puntos subsolares que hace que sea de día en Tarancón está entonces limitada por el horizonte de Tarancón (que es una propiedad local) y, por otra parte, por los trópicos de la Tierra que limitan la latitud del punto subsolar (y que es una propiedad global del planeta). Así podemos dibujar la región de la Tierra en la que el punto subsolar produce luz natural sobre Tarancón:
 Proyección acimutal centrada en Tarancón en la que se observa el cuadrángulo que limita la posición del punto subsolar para que sea de día en Tarancón. El cuadrángulo está limitado a derecha e izquierda el horizonte del observador y marca la evolución del amanecer y anochecer a lo largo del año. Arriba y abajo está limitado por los trópicos, estos limitan la latitud del punto subsolar.
Proyección acimutal centrada en Tarancón en la que se observa el cuadrángulo que limita la posición del punto subsolar para que sea de día en Tarancón. El cuadrángulo está limitado a derecha e izquierda el horizonte del observador y marca la evolución del amanecer y anochecer a lo largo del año. Arriba y abajo está limitado por los trópicos, estos limitan la latitud del punto subsolar.
La proyeccion acimutal varía según variamos la longitud geográfica y la latitud (o, mejor, dicho el valor absoluto de la latitud, ya que lo que importa es la distancia al Ecuador y no el hemisferio donde nos econtremos). Pero si variamos la longitud geográfica lo único que cambia es el paisaje, no la forma. Cambia la imagen de fondo de la Tierra sobre la que se dibujan las líneas pero no las líneas. Tarancón no es fundamentalmente diferente de Nápoles, solo lo es circunstancialmente.
La latitud sí hace variar las cosas. El punto subsolar está siempre está a 10000km de distancia cuando amanece, pero a lo largo del día se acerca más o menos al observador dependiendo de su latitud. Si estamos en la región subtropical dos días al año el Sol pasará por nuestras cabezas. Si estamos en las regiones polares apenas se pasará de esos 10000km o, incluso, a veces estará siempre más lejos y será noche perpetua.
Sin ser tan extremistas unos 16° de latitud más hacia el Ártico que Tarancón está la ciudad de Edimburgo:
 Proyección acimutal centrada en Edimburgo en la que se observa el cuadrángulo que limita la posición del punto subsolar para que sea de día en la ciudad británica. Obsérvese la diferencia con la imagen centrada en Tarancón.
Proyección acimutal centrada en Edimburgo en la que se observa el cuadrángulo que limita la posición del punto subsolar para que sea de día en la ciudad británica. Obsérvese la diferencia con la imagen centrada en Tarancón.
Y como ejemplo contrario podemos centrar la proyección en las islas Canarias obteniendo esta imagen en la que los límites laterales se acortan considerablemente:
 Proyección acimutal centrada en las islas Canarias en la que se observa el cuadrángulo que limita la posición del punto subsolar para que sea de día en el centro de la proyección.
Proyección acimutal centrada en las islas Canarias en la que se observa el cuadrángulo que limita la posición del punto subsolar para que sea de día en el centro de la proyección.
