En esta entrada no hay nada nuevo, consiste sólo en una pequeña digresión sobre las tendencias que pueden encontrarse en los datos de las encuestas de tiempo. En parte está motivada porque el público lector de estas entradas es variado y en muchos casos no está relacionado con la ciencia natural, que es mi ámbito de trabajo. En parte trata de explicar cómo veo o analizo algunos conjuntos de datos. En parte es un pequeño making-of.

Cuando en los medios de comunicación empezó a hablarse del «problema» de los husos españoles yo tenía el convencimiento de que la discusión olvidaba aspectos que tenían que ser importantes. Creía que además del papel de la longitud geográfica, la latitud tenía algo que decir, fundamentalmente a través de la insolación estival. Esto, aún hoy, es la parte más turbadora del estudio: la posibilidad de que la hipótesis con la que me acerco al problema sesgue su análisis.

Al descubrir las encuestas de uso de tiempo vi inmediatamente la oportunidad de comprobar esta idea: se trataba de encontrar parámetros relevantes a partir de las encuestas y probarlos en relación con alguna variable de origen geográfico como el desfase entre el huso horario y el huso geográfico (tesis que aparece en los medios de comunicación) o la latitud (que era mi preferencia).

Hay otra pequeña complicación cual es que hay que analizar eventos (por ejemplo la hora de entrada al trabajo) y duración de eventos (por ejemplo la jornada laboral). Un evento está trivialmente condicionado por la longitud geográfica y la rotación terrestre: eventos más orientales ocurren antes que eventos más occidentales. Esta trivialidad se elimina al transformar la hora civil (la que marca un reloj de pulsera) de un evento en hora solar (la que marca un reloj de Sol): en esta operación el huso horario desempeña un papel porque condiciona la hora civil. La duración de un evento, por contra, no depende de esta trivialidad: es o debe ser formalmente independiente de la longitud, el huso y el desfase.

Buscar y encontrar tendencias en eventos o en duración de eventos es también diferente. Voy a empezar refiriéndome el making-of de una relación relativa a un evento: la hora de entrada al trabajo y el amanecer invernal. Con las encuestas de uso de tiempo en mi ordenador determiné la hora civil de entrada al trabajo. De una base de datos recogí la información geográfica y representé la hora solar de entrada al trabajo frente a la latitud: los datos de España, Reino Unido e Italia que aparece en esta figura de mi primera entrada en Politikon.

Los datos de la figura muestran una tendencia clara. A más latitud entrada al trabajo más tardía. Podría haber calculado una recta de ajuste y un coeficiente de correlación (daría algo así como 0.9, todo un éxito) y habría quedaría chulo.

Habría sido un trabajo incompleto ya que faltaría el por qué, que fue la pregunta que me turbó cuando vi esta tendencia. Como mandan los cánones literarios fue bajo una ducha donde intuí la solución: los datos seguían al amanecer invernal. Salí de la ducha, abracé el albornoz, me senté en el ordenador y me puse a recordar cómo se calculaba esta hora. La coloqué en la gráfica y grité para mis adentros ¡eureka!

Una recta de ajuste o de tendencia depende de los datos experimentales y conlleva una referencia circular a ellos. Se pueden hacer pequeñas maravillas como el cuarteto de Anscombe, donde se muestra lo contrario: cómo datos de aspecto muy diferente pueden dar lugar a la misma tendencia estadística. El cuarteto plantea, a modo de un captcha, un problema de lógica difusa: no basta con recoger datos y pasarlos por la picadora de un programa informático y obtener coeficientes de correlación y pendientes. Hace falta otro tipo de intervención que se resume en un grito: visualize your data! También es una forma gráfica de plasmar eso de «hay mentiras, grandes mentiras y estadísticas».

El fenómeno natural (en este caso el amanecer invernal) es, por contra, independiente a priori de los datos experimentales. Sólo a posteriori se puede ver como se adaptan uno a lo otro y formular una tesis. En este caso y como resulta que el amanecer invernal es particularísimo por ser el más tardío del año se puede se puede decir que los trabajadores sienten aversión por entrar a trabajar antes de la salida del Sol.

Y así la recta de tendencia queda en un profundo olvido y lo único que queda es mejorar la gráfica; es decir presentar más eficientemente la información. Hay una evolución entre esa primera gráfica y la última, aunque sustancialmente sea lo mismo.

Repetiré y resumiré de nuevo lo importante de esas gráficas: superponen dos cosas independientes a priori; datos provenientes de las encuestas de uso del tiempo y las condiciones de luz ambiental en el invierno. Permite, a posteriori, confirmar una hipótesis trivial: que las personas gustan de trabajar con luz solar. La confirmación o demostración de hipótesis triviales o de verdades evidentes es también una tarea de la ciencia. Un ejemplo clásico es la demostración de la desigualdad triangular [esa cosa tan trivial de que el camino más corto entre dos puntos es la línea recta] a partir de los postulados de Euclídes.

Para las magnitudes de tipo duración de un evento el análisis es más fácil: se trata sólo de representarla frente al desfase del huso o, alternativamente, frente a la latitud. Ni la hora solar, ni el huso, ni el desfase intervienen inicialmente en la definición de la duración de un evento.

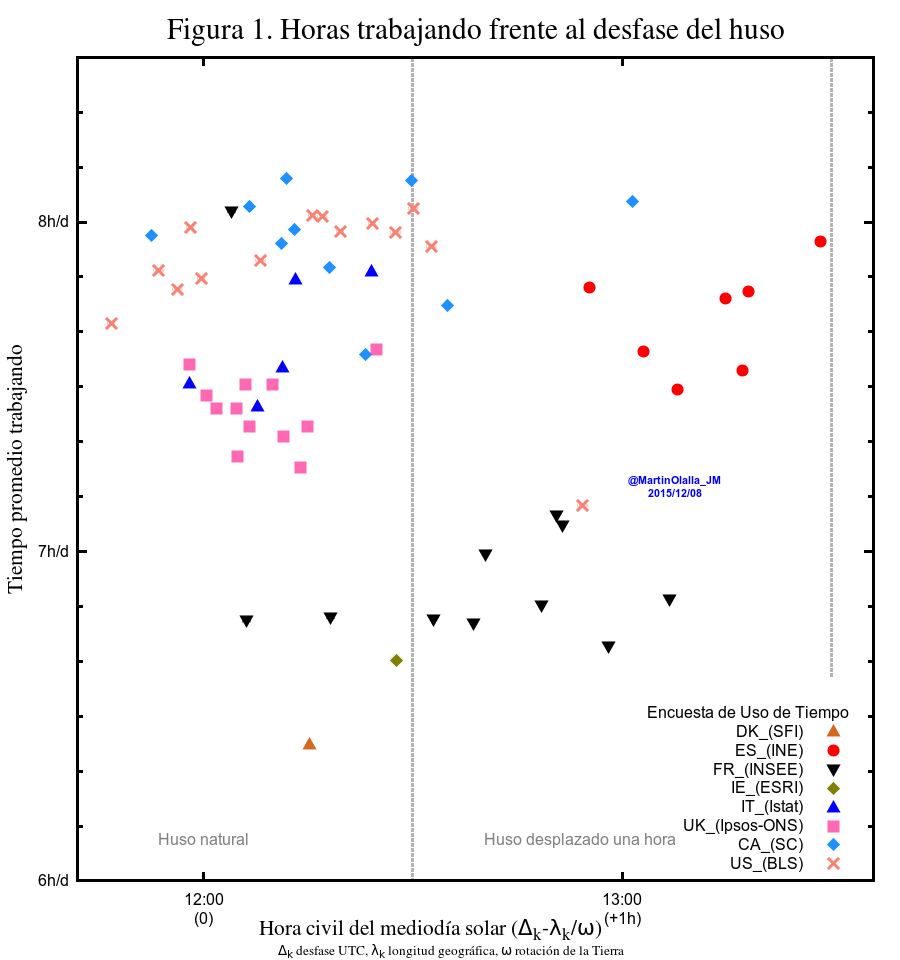
Muestro inicialmente este análisis para la duración de la jornada laboral: las horas diarias por trabajador que se emplean en la actividad laboral. He presentado la gráfica de la forma más limpia posible: eliminando las etiquetas y dejando sólo los puntos; es la forma mejor de no guiar los ojos del espectador por una tendencia.

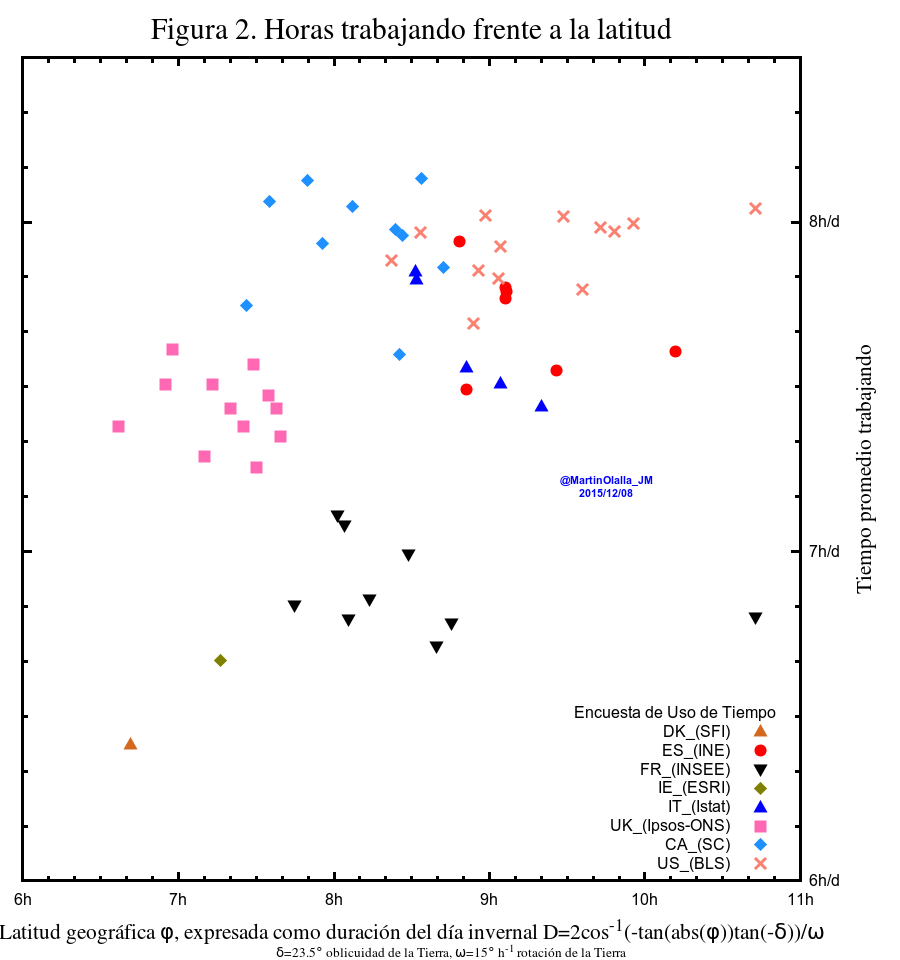Relación de la duración de la jornada laboral determinada como horas de trabajo consumidas por día y trabajador frente al desfase entre el huso geográfico y horario (a la izquierda) y frente a la latitud (derecha).

Cualquiera es libre de ver tendencias en la figura 1. Por ejemplo la que tienen los datos de Dinamarca, Irlanda, Francia y España: a más defase más jornada laboral. Podría pasar el rodillo estadístico y determinar una recta y su coeficiente de correlación (que sería excelente). Es poco probable que signifique algo. No soy experto en estos temas pero intuyo que probablemente sólo estamos observando la diferente regulación del mercado laboral en esos países. Recuerdo, por ejemplo, discusiones en los periódicos sobre la ley francesa de las 35 horas semanales (siete horas diarias de lunes a viernes).

Por otra parte el conjunto de datos formado por Reino Unido, Italia, Estados Unidos, Canadá y España muestran que la magnitud representada es bastante insesible al valor del desfase: si dibujara una recta de tendencia esta sería muy próxima a la horizonal.

La misma discusión y conclusión se obtiene al hablar de la latitud (figura 2) aunque la discutiré con más detalle posteriormente.

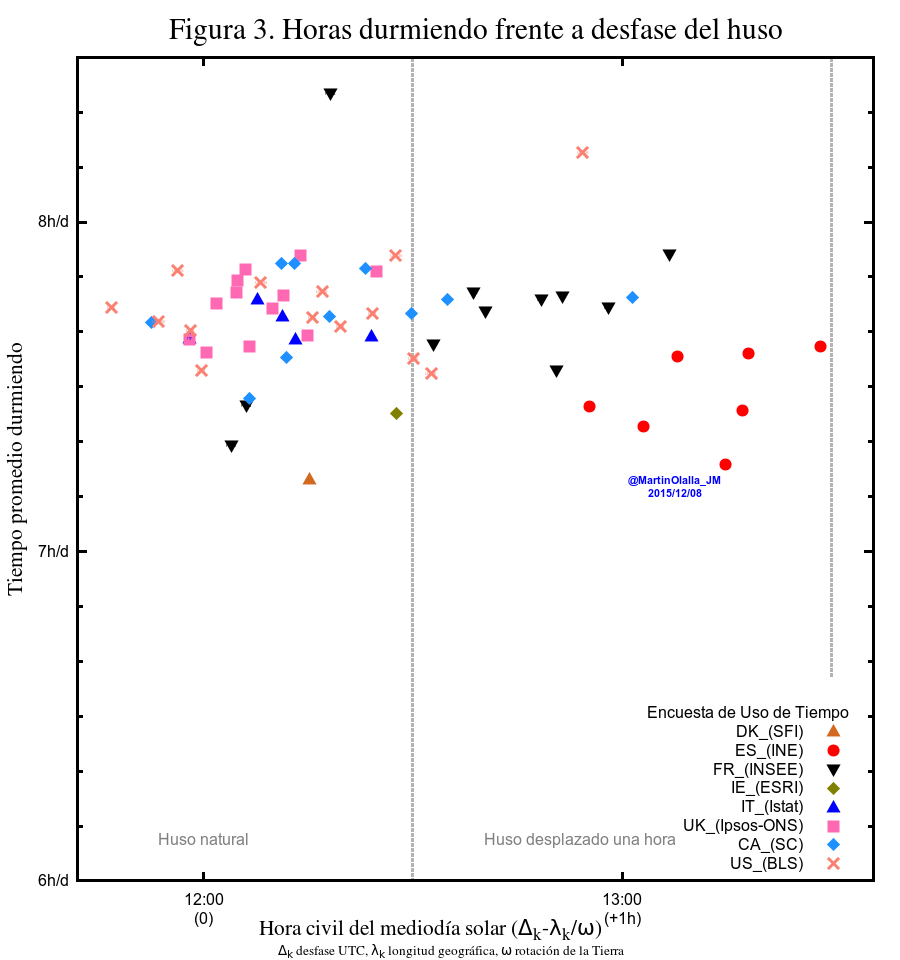
La siguiente gráfica representa las horas diarias de sueño por trabajador de cada encuesta. Recordarán las intensas admoniciones sobre lo poco que duermen los trabajadores españoles. Sin embargo los datos muestran que dormimos tan poco como muchos. También es difícil encontrar una tendencia. Casi todos ellos caen en una banda de media hora. Podemos flagelarnos y quedarnos con que los datos españoles estén en el segmento más bajo (aunque incluso la muy módelica Dinamarca obtenga valores menores) pero a causa de qué.

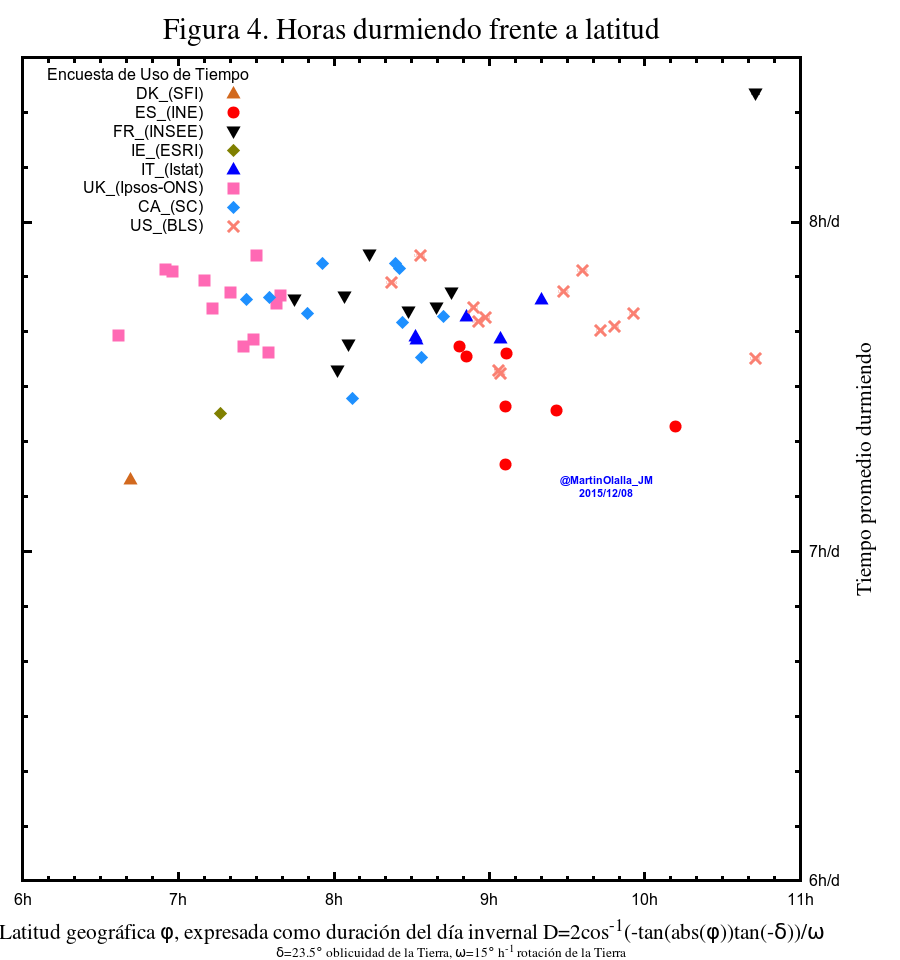Relación de la duración del sueño determinada como horas de sueño consumidas por día y trabajador frente al desfase entre el huso geográfico y horario (a la izquierda) y frente a la latitud (derecha).

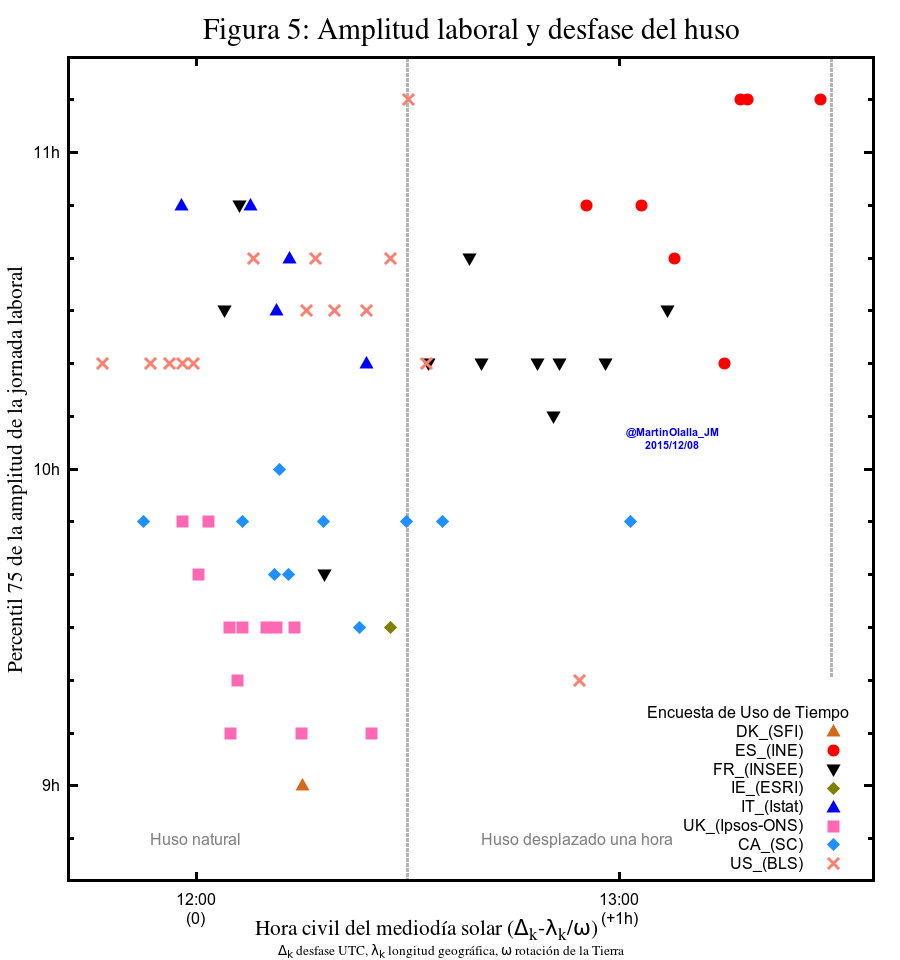
El tercer conjunto apareció en la entrada anterior y representa el percentil 75 de la amplitud laboral frente al desfase y frente a la latitud. Ahora la muestro sin etiquetas, para que la figura quede más limpia.

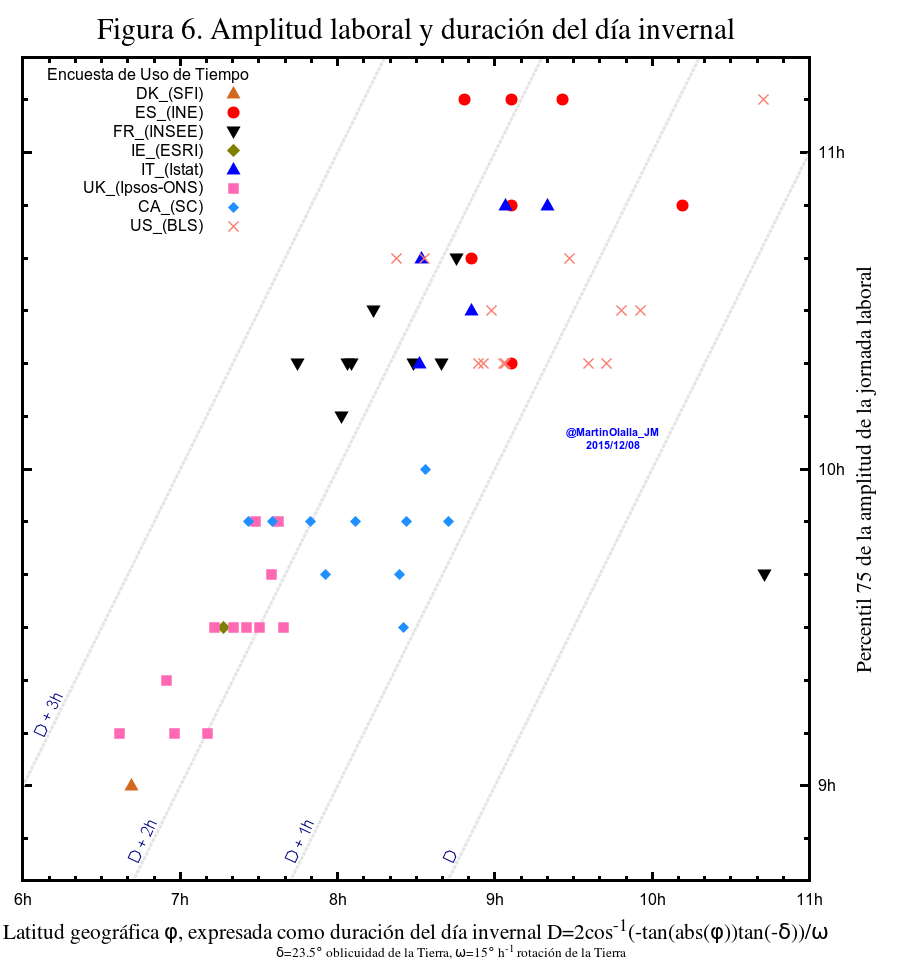Relación del percentil 75 del amplitud laboral frente al desfase del huso geográfico y horario (a la izquierda) y frente a la latitud (derecha).

En la figura 5 puede verse de nuevo una tendencia lineal entre el desfase y los datos españoles, canadienses y británicos pero no creo que sea la lectura más correcta por dos motivos. Primero porque hay un hueco entorno a las diez horas que separa los datos de Estados Unidos, Francia, Italia y España de los de Canadá, Reino Unido, Irlanda y Dinamarca. Es difícil saber si ese hueco existiría independientemente del desfase porque sólo una región con el huso desplazado en el grupo inverior de datos. Se trata de la provincia canadiense de Saskatchewan; el dato estadounidense corresponde al estado de Alaska que tiene unas características muy singulares. El segundo argumento es que dentro de cada uno de esos subcojuntos los datos parecen insensibles al desfase.

Centrándonos en países europeos los valores de Italia, Francia y España (tres países relativamente parecidos en tamaño y situación geográfica) son similares aún cuando el desfase del huso varía mucho entre los tres.

Cuando se analiza la latitud (o la duración del día invernal) se obtiene una relación causal más probable. Con todo es una relación discutible: por ejemplo Canadá y Francia comparten latitud y tienen valores diferentes de la propiedad. O los datos de Francia y Estados Unidos presentan unos valores similares de amplitud laboral a valores diferentes de latitud.

No obstante la ventaja de esta gráfica es que se pueden trazar líneas naturales (es decir, líneas no relacionadas en modo alguno con los datos sociales) que agrupan a los valores obtenidos y proporcionan una explicación plausible: casi todos los valores del percentil 75 de la distribución de la amplitud laboral en regiones con latitud supratropical (de la península Ibérica hacia arriba) caen entre una hora más que el día invernal y dos horas y media más que el día invernal.

Hay diferencias entre los países europeos y americanos: los americanos están marcadamente en la banda entre una y dos horas más que la duración del día invernal. Los europeos exceden con más frecuencia de las dos horas de duraciónd el día invernal. Esto apunta a diferencias culturales o relacionadas con la regulación de los mercados laborales.

La recta que representa dos horas más que la duración del día invernal muestra jornadas que empiezan con el amanecer invernal y, con sus descansos correspondientes, se extiende hasta dos horas después del añochecer invernal. O jornadas que empiezan una hora antes del amanecer invernal y se extienden hasta dos horas después del anochecer invernal.

La correspondencia entre los valores más altos de las regiones españolas (casi once horas de amplitud laboral para nueve horas de día invernal) y los valores más bajos de Dinamarca y el norte del Reino Unido (unas nueve horas de amplitud laboral para siete horas de día invernal) es casi completa y tiene una explicación lógica en el hecho de que la actividad laboral está condicionada por la luz invernal. Los trabajadores septentrionales no tiene oportunidad de tener jornadas más amplias porque no hay actividad laboral. Por contra, los trabajadores meridionales tienen más oportunidades (pero no la obligación) de tener jornadas más amplias simplemente porque hay más mercado de horas laborables.

Ahora estoy en disposción de retomar la discusión de la figura 2 en la que se representa la jornada laboral media frente a la duración del día invernal. Al igual que en la figura 6, en la figura 2 también se pueden trazar líneas naturales que representen la duración del día. No lo hice antes para no guiar los ojos del lector con esa líneas, pero sí lo hago en la siguiente figura:

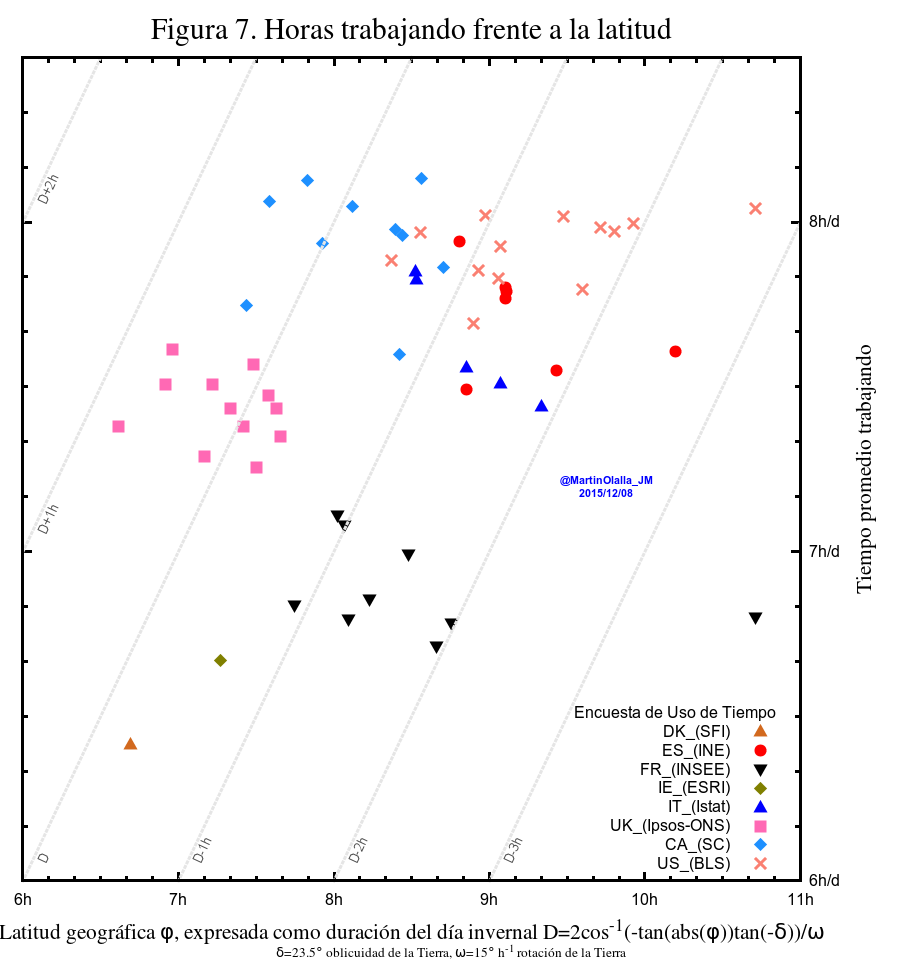
Lo mismo que la figura 2 pero con líneas naturales que expresan desfases con la duración del día invernal.

Las líneas naturales de la figura 7 no explican tendencia alguna de la jornada laboral con la latitud. Otros factores externos, como la regulación laboral local son los que determinan estos valores. Pero por comparación, la figura 7 sí refuerza el argumento de que en la figura 6 sí hay una tendencia: en la figura 6 los datos sí se disponen de forma correlacionada parecida a la línea natural. Para los amantes de las estadísticas comentaré que el ajuste lineal de los datos de la figura 6 y 7 obtiene coeficientes de correlación de varios nueves ¡en ambos casos! Es otro ejemplo del visualize [and understand] your data!

Lo que sí hacen las líneas de la figura 7 es explicar los datos en la relación del orto y ocaso invernal con el inicio y del fin de la jornada laboral que he tratado en entradas anteriores. En España, Francia y Estados Unidos la jornada es claramente más corta que el día invernal. Aún contando con el descanso para almorzar es posible que el inicio y fin de la jornada laboral no se introduzcan mucho en la zona crespuscular.

La jornada laboral en Irlanda, Dinamarca y Canadá casi coincide con la duración del día invernal; si contamos con el descanso a mediodía es inevitable que se introduzcan en zona crespucular, sea matinal o vespertina. Finalmente en Reino Unido la jornada laboral tiende a exceder la duración del día invernal y unido al descanso es inevitable que la jornada laboral se extienda a zonas más profundas del crespúsculo vespertino, con el huso horario actual, o del crespúculo matinal, si adelantaran el huso.

En resumen, el huso horario y su desfase con el huso geográfico están sobrevalorados en la discusión actual sobre los horarios. Es difícil encontrar tendencia alguna entre las magnitudes relevantes que se extraen de las encuestas de uso del tiempo y ese desfase. En cambio no es extraño encontrarlas con la latitud.

Referencias

• Det Nationale Forskningscenter for Velfærd, Danske Tidsanvendelseundersøgelsen. Centre for Survey and Survey/Register Data [distribuiddor]. 2001.
• Instituto Nacional de Estadística, Encuesta de Empleo del Tiempo 2009-2010.
• L’Institut National de la Statistique et des Études Économiques, Enquête Emploi du Temps et Décisions dans les Couples 2009-2010.
• Economic and Social Research Institute, The Irish National Time-Use Survey Irish Social Science Data Archive [distribuidor] 2005.
• L’Istituto nazionale di statistica (Istat) Uso del tempo 2008/09
• Ipsos-RSL y Office of National Statistics United Kingdom Time Use Survey 2000 [computer file]. Tercera edición. Colchester, Essex: UK Data Archive [distribuidor]. Septiembre 2003.
• Statistics Canada/Statisque Canada, General Social Survey, Time Use. Cycle 19, 2005. 2006.
• Bureau of Labor Statistics American Time Use Survey [archivo multianual 2003-2012]. US Departament of Labor. 2013